class: center, middle, inverse, title-slide # 3.2: Voting II: Ignorance & Irrationality ## ECON 410 · Public Economics · Spring 2020 ### Ryan Safner<br> Assistant Professor of Economics <br> <a href="mailto:safner@hood.edu"><i class="fa fa-paper-plane fa-fw"></i> safner@hood.edu</a> <br> <a href="https://github.com/ryansafner/publicS20"><i class="fa fa-github fa-fw"></i> ryansafner/metricsf19</a><br> <a href="https://publicS20.classes.ryansafner.com"> <i class="fa fa-globe fa-fw"></i> publicS20.classes.ryansafner.com</a><br> --- # Major Actors in a Liberal Democracy .pull-left[ - .hi[Voters] express preferences through elections - .hi[Special interest groups] provide additional information and advocacy for lawmaking - .hi[Politicians] create laws reflecting voter and interest gorup preferences - .hi[Bureaucrats] implement laws according to goals set by politicians ] .pull-right[ .center[  ] ] --- # Two Questions for the Next Few Weeks .pull-left[ 1. What .hi-purple[incentives] does each group face? - How is this affected by the .hi-purple[institutions] we set up? 2. How does this .hi-purple[explain policy and behavior] we see in the real world? ] .pull-right[ .center[  ] ] --- # *Voters* in a Liberal Democracy .pull-left[ - .hi[Voters] express preferences through elections - Voters as economic agents: 1. **Choose:** .hi-purple[ < a candidate >] 2. **In order to maximize:** .hi-green[< utility >] 3. **Subject to:** .hi-red[< constraints? >] ] .pull-right[ .center[  ] ] --- # Constraints of Voting: An Inconvenience Store .pull-left[ .pull-left[ .center[  Bundle "D" ] ] .pull-right[ .center[  Bundle "R" ] ] ] .pull-right[ - Recall the spatial model of voting: - Each candidate represents a **bundle** of policy positions - Voters vote for candidate **closest** to their ideal point - Suppose "D" wins - Can we say that voters prefer eggs `\(\succ\)` sausage? ] --- # Constraints of Voting: An Inconvenience Store .pull-left[ .pull-left[ .center[  Bundle "D" ] ] .pull-right[ .center[  Bundle "R" ] ] ] .pull-right[ - Recall the spatial model of voting: - Each candidate represents a **bundle** of policy positions - Voters vote for candidate **closest** to their ideal point ] --- class: inverse, center, middle # Rational Ignorance --- # The Collective Action Problem of Democracy .pull-left[ .center[  ] ] .pull-right[ - Citizens vote in politicians to enact various laws that citizens prefer -- and vote politicians out of office if they fail to deliver - A .hi[collective action problem]: citizens need to monitor the performance of politicians and bureaucrats to ensure government serves voters' interests ] --- # The Collective Action Problem of Democracy .pull-left[ .center[  ] ] .pull-right[ - Voting is **instrumental** in enacting voters' preferences into policy - Good governance is a .hi-purple[public good]: an individual citizen enjoys **small fraction of benefit** created - Additionally, policies & elections depend on many millions of people - Individual bears a **private cost** of informing self and participating - Hence, a .hi[free-rider problem] ] --- # The Rational Calculus of Voting .pull-left[ .center[  ] ] .pull-right[ - A rational individual will vote iff: `$$p(B)+W > C$$` - `\(B\)`: perceived net benefits of candidate `\(X\)` over `\(Y\)` - `\(p\)`: probability individual vote will affect the outcome of the election - `\(W\)`: individual's utility derived from voting regardless of the outcome (e.g. civic duty, "warm glow," etc) - `\(C\)`: marginal cost of voting ] --- # The Rational Calculus of Voting .pull-left[ .center[  ] ] .pull-right[ - A rational individual will vote iff: `$$p(B)+W > C$$` .smaller[ - `\(p \approx 0\)` - Outcome requires many votes - `\(B\)` is a public good - Get small fraction of total benefit - `\(C>0\)` - Cost of informing oneself and voting informed ] ] --- # The Rational Calculus of Voting .pull-left[ .center[  ] ] .pull-right[ - A rational individual will vote iff: `$$p(B)+W > C$$` - If citizens are *purely* rational, `\(W= 0\)` - Citizens then vote if `\(p(B) > C\)` - Prediction: **rational citizen does not vote** ] --- # Voter Turnout: Presidential Elections | Year | Turnout of Elligible Voters| |------|----------:| | 2016 | 55.7% | | 2012 | 54.9% | | 2008 | 58.2% | | 2004 | 55.7% | | 2000 | 50.3% | | 1996 | 49.0% | | 1992 | 55.2% | .source[Sources: [Wikipedia](https://en.wikipedia.org/wiki/Voter_turnout_in_the_United_States_presidential_elections), U.S. Census Bureau, Bipartisan Policy Center] --- # The Rational Calculus of Voting .pull-left[ .center[  ] ] .pull-right[ - A rational individual will vote iff: `$$p(B)+W > C$$` - Now suppose, `\(D > 0\)` - Citizens then vote if `\(D > C\)` - More importantly, the voter votes *regardless* of the positions of the candidates! - Vote for *non-rational* reasons: "more presidential looking," "taller," "a better temperament," etc. ] --- # The Rational Calculus of Voting .pull-left[ .center[  ] ] .pull-right[ - Many *do* vote, even at significant personal cost! - .hi-purple["Expressive voting"]: people vote to express identity, solidarity, tribalism, preferences, etc - Voting as a .hi-purple[pure consumption good], not an instrumental investment to achieve policy preferences ] --- # Rational Ignorance .pull-left[ .center[  ] ] .pull-right[ - Model predicts .hi[rational ignorance] - Not necessarily *no* voting, but - Less than maximum turnout - Voting **not for instrumental, "rational" reasons**, but for non-rational reasons ] --- # Rational Ignorance .left-column[ .center[  Winston Churchill 1874-1965 ] ] .right-column[ > "The best argument against democracy is a five minute conversation with the average voter." ] --- # Rational Ignorance .center[  ] .source[Somin, Ilya, 2014, *Democracy and Political Ignorance*] --- # Rational Ignorance .center[  ] .source[Somin, Ilya, 2014, *Democracy and Political Ignorance*] --- class: inverse, center, middle # Rational Irrationality --- # The Miracle of Aggregation .pull-left[ .hi[Miracle of Aggregation]: under the right conditions, large groups can pick reach the optimal outcome, even if each individual is unlikely to choose the optimal outcome ] .pull-right[ .center[  ] ] --- # The Miracle of Aggregation .pull-left[ .hi[Miracle of Aggregation]: under the right conditions, large groups can pick reach the optimal outcome, even if each individual is unlikely to choose the optimal outcome ] .pull-right[ .center[  ] ] --- # The Miracle of Aggregation .pull-left[ Some basic statistics of sampling: - .hi-purple[Central Limit Theorem]: With large enough `\(n\)`, distribution of outcomes is approximately normal - Extreme "errors" on either side of the mean cancel out such that the sample mean is, on average, an unbiased estimator of the truth ] .pull-right[ .center[  ] ] --- # The Miracle of Aggregation .pull-left[ If there are .hi[systematic biases], or individuals are all likely to be .hi-purple[wrong in the same way], the mean is no longer unbiased! ] .pull-right[ .center[  ] ] --- # The Miracle of Aggregation: Juries .pull-left[ Why do we have **trial by jury** instead of an **expert judge** decide most cases? ] .pull-right[ .center[  ] ] --- # The Miracle of Aggregation: Juries .pull-left[ - Suppose an expert judge is correct 90% of the time `$$Pr(J=Wrong)=0.10$$` ] .pull-right[ .center[  ] ] --- # The Miracle of Aggregation: Juries .pull-left[ - Suppose an expert judge is correct 90% of the time `$$Pr(J=Wrong)=0.10$$` - Suppose each individual juror, `\(i\)`, is no better than random `$$Pr(i=Wrong)=0.50$$` ] .pull-right[ .center[  ] ] --- # The Miracle of Aggregation: Juries .pull-left[ - Suppose an expert judge is correct 90% of the time `$$Pr(J=Wrong)=0.10$$` - Suppose each individual juror, `\(i\)`, is no better than random `$$Pr(i=Wrong)=0.50$$` `$$\begin{align*} Pr(\text{All } i=Wrong)&= \prod^{n}_{i=1} 0.50\\ &=0.50^{12}=0.0002\\ \end{align*}$$` ] .pull-right[ .center[  ] ] --- # The Miracle of Aggregation: Juries .pull-left[ - The decision rule for criminal cases at common law is **unanimous consent** of a jury **beyond a reasonable doubt** - Minimize external costs of false conviction of innocents `$$Pr(\text{All } i=wrong) < Pr(J=wrong)$$` ] .pull-right[ .center[  ] ] --- # Condorcet Jury Theorem .left-column[ .center[  .smallest[ Marquis of Condorcet 1743--1794 ] ] ] .right-column[ - Suppose there is a correct outcome (e.g. innocent or guilty) and a group wishes to reach a decision by majority rule - Each voter has an independent probability `\(p_i\)` of voting for the correct decision - How many voters should we include in the group? .source[M. Le Marquis de Condorcet, *Essai Sur L'Application de L'Analyse a la Probabilite des Decisions Rendues a la pluralite des voix*] ] --- # Condorcet Jury Theorem .left-column[ .center[  .smallest[ Marquis of Condorcet 1743--1794 ] ] ] .right-column[ - .hi[Condorcet Jury Theorem]: if `\(p_i > 0.50\)`, then as `\(n \to \infty\)`, `\(p(Correct) \to 1\)` - Adding more voters increases the probability of the correct outcome - Note: if `\(p_i < 0.50\)`, adding more voters *decreases* the probability of the correct outcome! - Optimal jury consists of `\(n=1\)` .source[M. 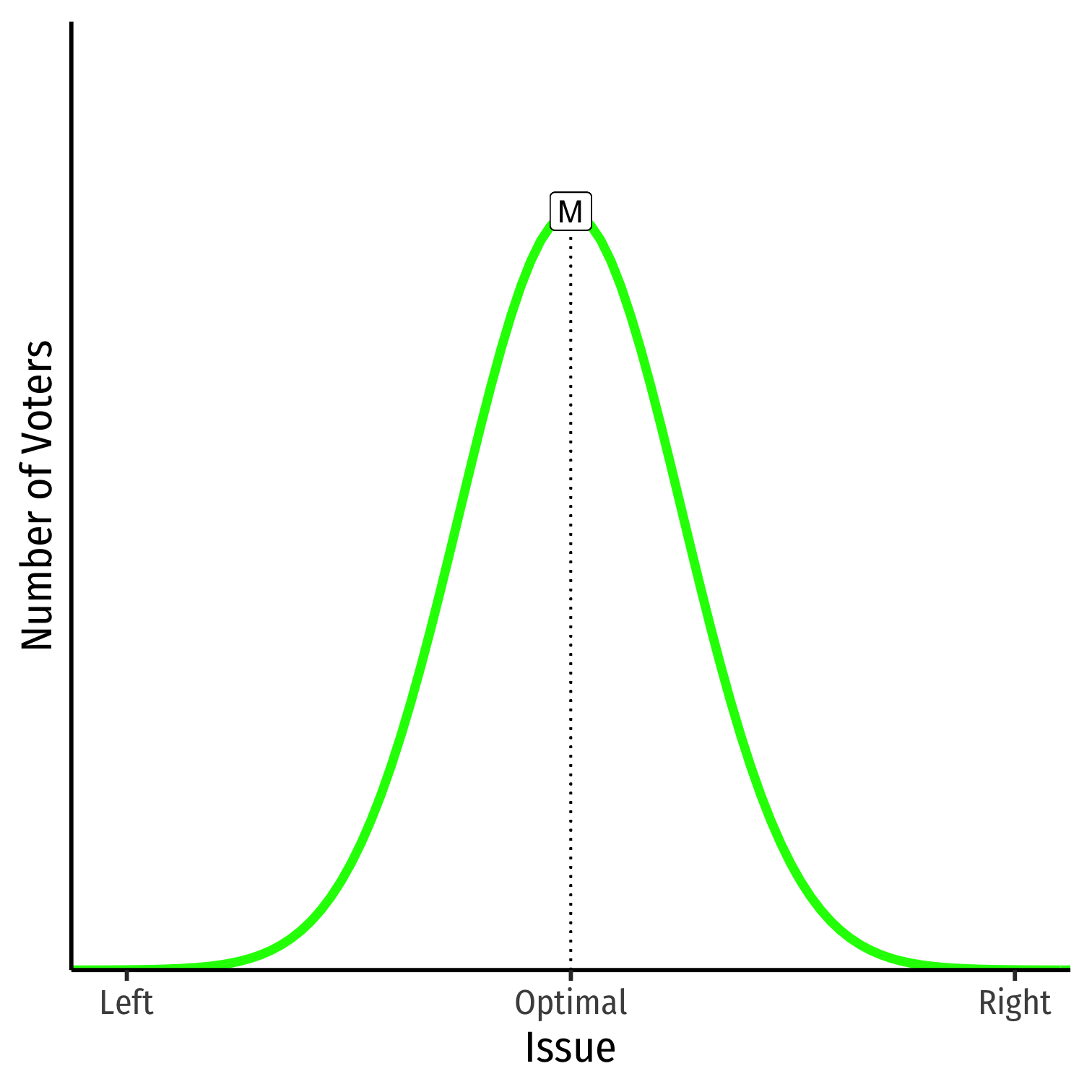Le Marquis de Condorcet, *Essai Sur L'Application de L'Analyse a la Probabilite des Decisions Rendues a la pluralite des voix*] ] --- # The Miracle of Aggregation and MVT .pull-left[ <img src="3.2-slides_files/figure-html/unnamed-chunk-1-1.png" width="504" style="display: block; margin: auto;" /> ] .pull-right[ - Applied to mass election: - Even if individual voters are rationally ignorant, individual votes on either side of optimum cancel out - Socially optimum policy remains at the median, and is thus, the winning policy enacted ] --- # The Miracle of Aggregation and MVT .pull-left[ <img src="3.2-slides_files/figure-html/unnamed-chunk-2-1.png" width="504" style="display: block; margin: auto;" /> ] .pull-right[ - 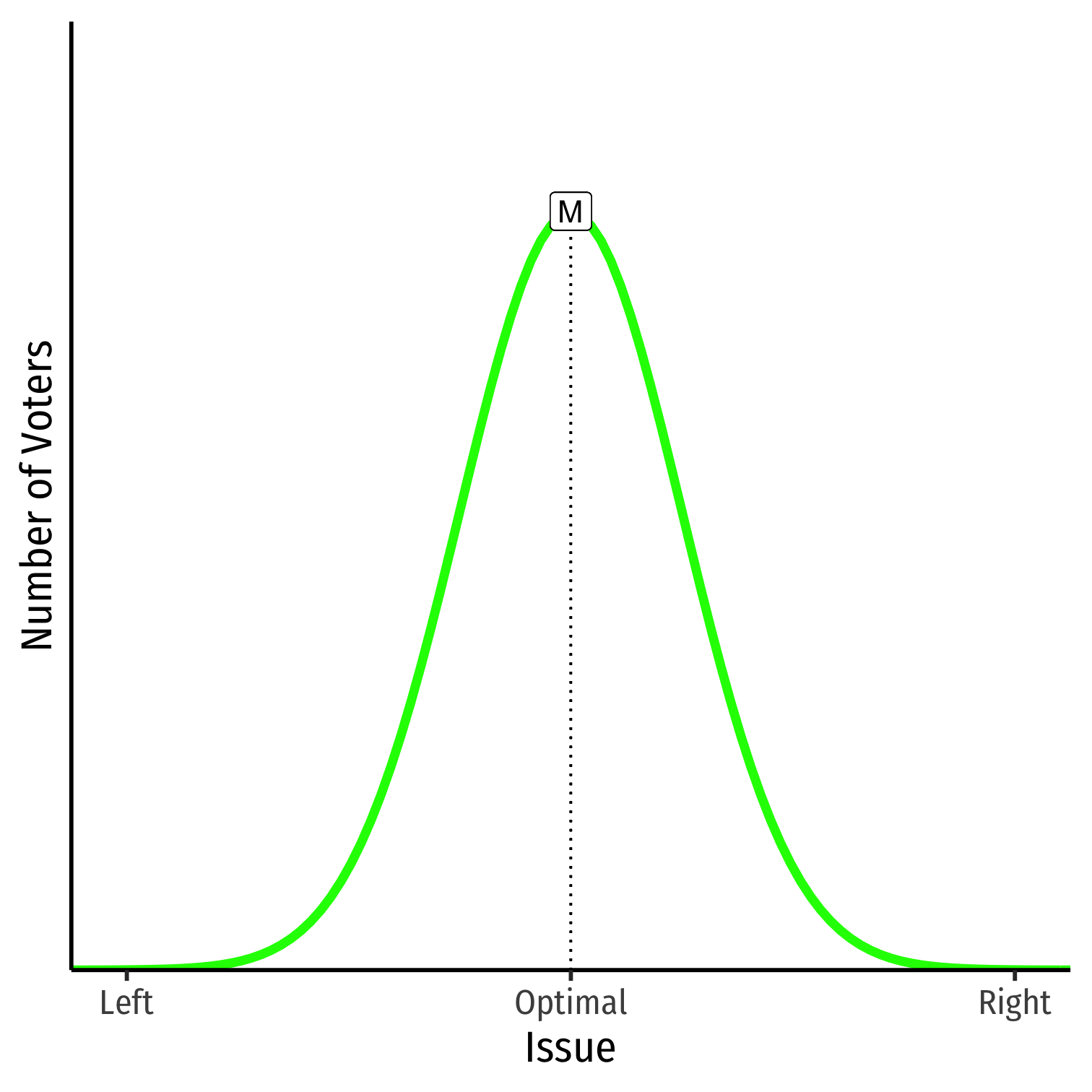Applied to mass election: - Even if individual voters are rationally ignorant, individual votes on either side of optimum cancel out - Socially optimum policy remains at the median, and is thus, the winning policy enacted - ...so long as there are not systematic biases ] --- # The Miracle of Aggregation and MVT .pull-left[ <img src="3.2-slides_files/figure-html/unnamed-chunk-3-1.png" width="504" style="display: block; margin: auto;" /> ] .pull-right[ - .hi-purple[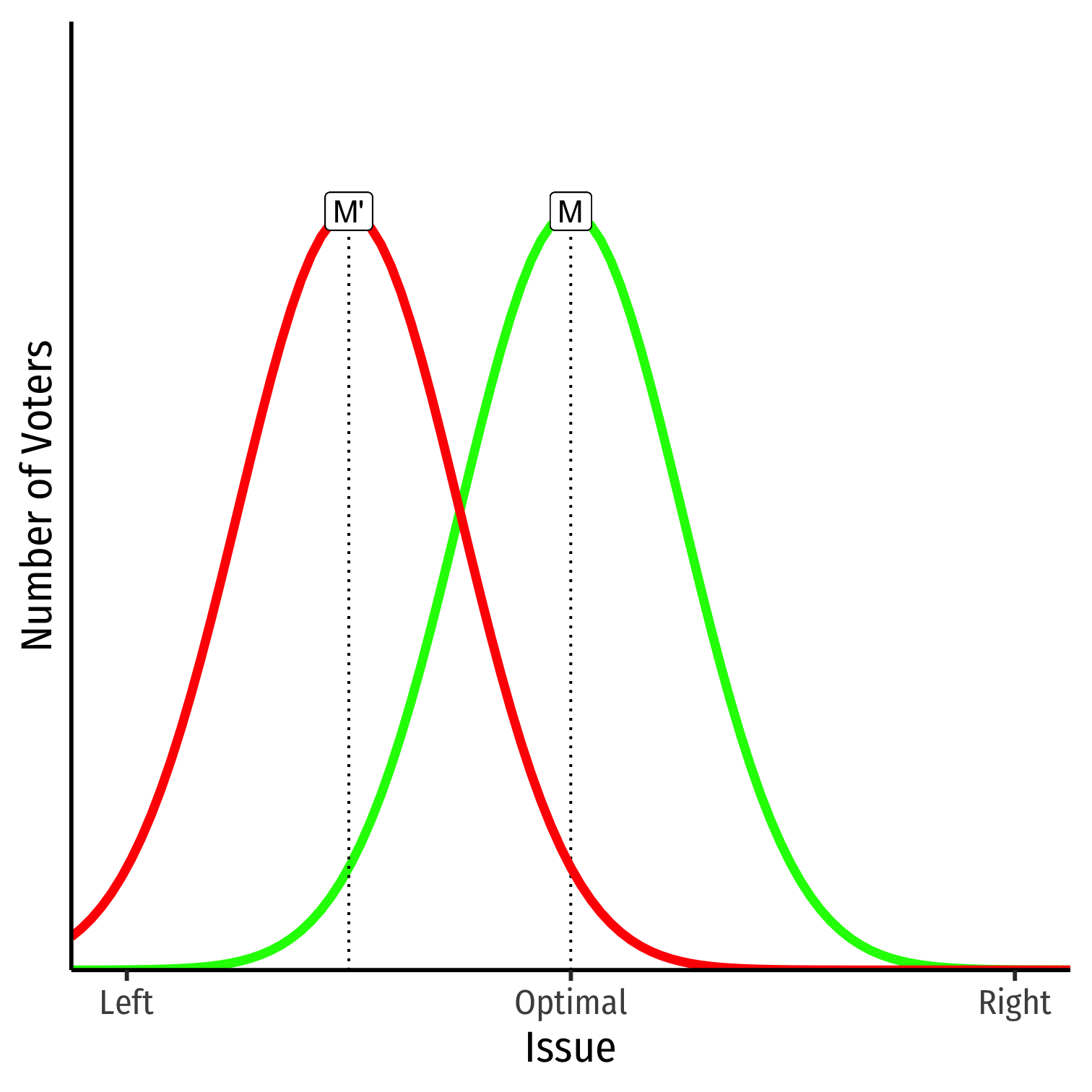If there are systematic biases, the median (winning) policy platform will _not_ be the socially optimal policy] ] --- # Systematically-Biased Beliefs .pull-left[ .center[  ] ] .pull-right[ - People **do** have systematically biased beliefs? - Caplan: 1. Anti-market bias 2. Anti-foreign bias 3. Make-work bias 4. Pessimistic bias ] --- # Systematically-Biased Beliefs .pull-left[ .center[  ] ] .pull-right[ - Think about your own experience taking economics classes! - They probably have disabused you of some things you thought before taking them! ] --- # Rational Irrationality .left-column[ .center[  Bryan Caplan 1971- ] ] .right-column[ - .hi[Irrationality] is a consumption good that protects our comforting beliefs from reality or scrutiny - Many biases are .hi-purple[costly to indulge]: anti-vaxx, faith healing, quack medicine, etc - have to face tradeoffs between maintaining belief and suffering a cost ] --- # Rational Irrationality .left-column[ .center[  Bryan Caplan 1971- ] ] .right-column[ .center[  ] ] .source[Caplan, Bryan, 2001, "Rational Ignorance versus Rational Irrationality," *Kyklos* 54: 3-26] --- # Rational Irrationality .left-column[ .center[  Bryan Caplan 1971- ] ] .right-column[ - But in many areas (politics, religion, astrology), the "cost" of irrationality is zero! - .hi[Irrationality] in politics: beliefs that are non-falsifiable, false, or biased - Voting often signals an identity and membership in a particular tribe (ideology, identity politics, etc) - Having your biases questioned is **painful**!! .source[Caplan, Bryan, 2007, *The Myth of the Rational Voter*] ] --- # Rational Irrationality: Implications .left-column[ .center[  Bryan Caplan 1971- ] ] .right-column[ - .hi-purple[It's rational for individuals to maintain irrational (objectively wrong) beliefs about politics] - Actual policies are not necessarily bad because of corruption, special interests, backroom deals, etc - Voters might be getting exactly what they want! - "The median voter is a moderate National Socialist" .source[Caplan, Bryan, 2007, *The Myth of the Rational Voter*] ] --- # Rational Irrationality: Implications .left-column[ .center[  H.L. Mencken 1880-1956 ] ] .right-column[ > "Democracy is the theory that the common people know what they want, and deserve to get it good and hard." .source[Mencken, H. L, 1926, *Notes on Democracy*] ]